A central chapter that crystallizes all my work. In forth. Skin in the Game
Time to explain ergodicity, ruin and (again) rationality. Recall from the previous chapter that to do science (and other nice things) requires survival but not the other way around?Consider the following thought experiment.
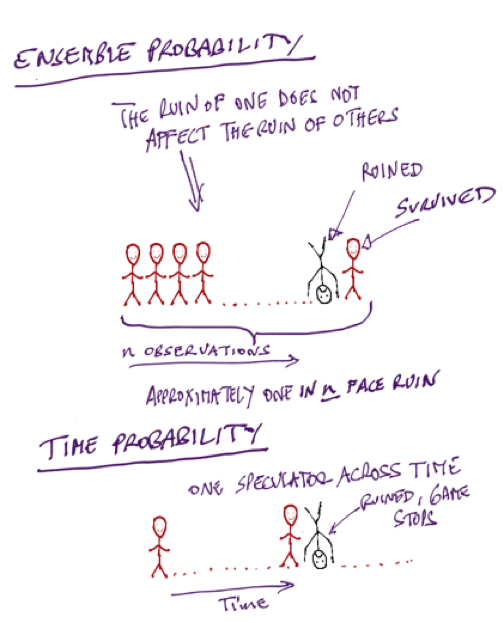
First case, one hundred persons go to a Casino, to gamble a certain set amount each and have complimentary gin and tonic –as shown in the cartoon in Figure x. Some may lose, some may win, and we can infer at the end of the day what the “edge” is, that is, calculate the returns simply by counting the money left with the people who return. We can thus figure out if the casino is properly pricing the odds. Now assume that gambler number 28 goes bust. Will gambler number 29 be affected? No.
You can safely calculate, from your sample, that about 1% of the gamblers will go bust. And if you keep playing and playing, you will be expected have about the same ratio, 1% of gamblers over that time window.
Now compare to the second case in the thought experiment. One person, your cousin Theodorus Ibn Warqa, goes to the Casino a hundred days in a row, starting with a set amount. On day 28 cousin Theodorus Ibn Warqa is bust. Will there be day 29? No. He has hit an uncle point; there is no game no more.
No matter how good he is or how alert your cousin Theodorus Ibn Warqa can be, you can safely calculate that he has a 100% probability of eventually going bust.
The probabilities of success from the collection of people does not apply to cousin Theodorus Ibn Warqa. Let us call the first set ensemble probability, and the second one time probability (since one is concerned with a collection of people and the other with a single person through time). Now, when you read material by finance professors, finance gurus or your local bank making investment recommendations based on the long term returns of the market, beware. Even if their forecast were true (it isn’t), no person can get the returns of the market unless he has infinite pockets and no uncle points. The are conflating ensemble probability and time probability. If the investor has to eventually reduce his exposure because of losses, or because of retirement, or because he remarried his neighbor’s wife, or because he changed his mind about life, his returns will be divorced from those of the market, period.
We saw with the earlier comment by Warren Buffet that, literally, anyone who survived in the risk taking business has a version of “in order to succeed, you must first survive.” My own version has been: “never cross a river if it is on average four feet deep.” I effectively organized all my life around the point that sequence matters and the presence of ruin does not allow cost-benefit analyses; but it never hit me that the flaw in decision theory was so deep. Until came out of nowhere a paper by the physicist Ole Peters, working with the great Murray Gell-Mann. They presented a version of the difference between the ensemble and the time probabilities with a similar thought experiment as mine above, and showed that about everything in social science about probability is flawed. Deeply flawed. Very deeply flawed. For, in the quarter millennia since the formulation by the mathematician Jacob Bernoulli, and one that became standard, almost all people involved in decision theory made a severe mistake. Everyone? Not quite: every economist, but not everyone: the applied mathematicians Claude Shannon, Ed Thorp, and the physicist J.-L. Kelly of the Kelly Criterion got it right. They also got it in a very simple way. The father of insurance mathematics, the Swedish applied mathematician Harald Cramér also got the point. And, more than two decades ago, practitioners such as Mark Spitznagel and myself build our entire business careers around it. (I personally get it right in words and when I trade and decisions, and detect when ergodicity is violated, but I never explicitly got the overall mathematical structure –ergodicity is actually discussed in Fooled by Randomness). Spitznagel and I even started an entire business to help investors eliminate uncle points so they can get the returns of the market. While I retired to do some flaneuring, Mark continued at his Universa relentlessly (and successfully, while all others have failed). Mark and I have been frustrated by economists who, not getting ergodicity, keep saying that worrying about the tails is “irrational”.
Now there is a skin in the game problem in the blindness to the point. The idea I just presented is very very simple. But how come nobody for 250 years got it? Skin in the game, skin in the game.
It looks like you need a lot of intelligence to figure probabilistic things out when you don’t have skin in the game. There are things one can only get if one has some risk on the line: what I said above is, in retrospect, obvious. But to figure it out for an overeducated nonpractitioner is hard. Unless one is a genius, that is have the clarity of mind to see through the mud, or have such a profound command of probability theory to see through the nonsense. Now, certifiably, Murray Gell-Mann is a genius (and, likely, Peters). Gell-Mann is a famed physicist, with Nobel, and discovered the subatomic particles he himself called quarks. Peters said that when he presented the idea to him, “he got it instantly”. Claude Shannon, Ed Thorp, Kelly and Cramér are, no doubt, geniuses –I can vouch for this unmistakable clarity of mind combined with depth of thinking that juts out when in conversation with Thorp. These people could get it without skin in the game. But economists, psychologists and decision-theorists have no genius (unless one counts the polymath Herb Simon who did some psychology on the side) and odds are will never have one. Adding people without fundamental insights does not sum up to insight; looking for clarity in these fields is like looking for aesthetic in the attic of a highly disorganized electrician.
Continue reading on Medium: https: // medium. com/ incerto / the-logic- of -risk- taking- 107bf41029d3